感知器
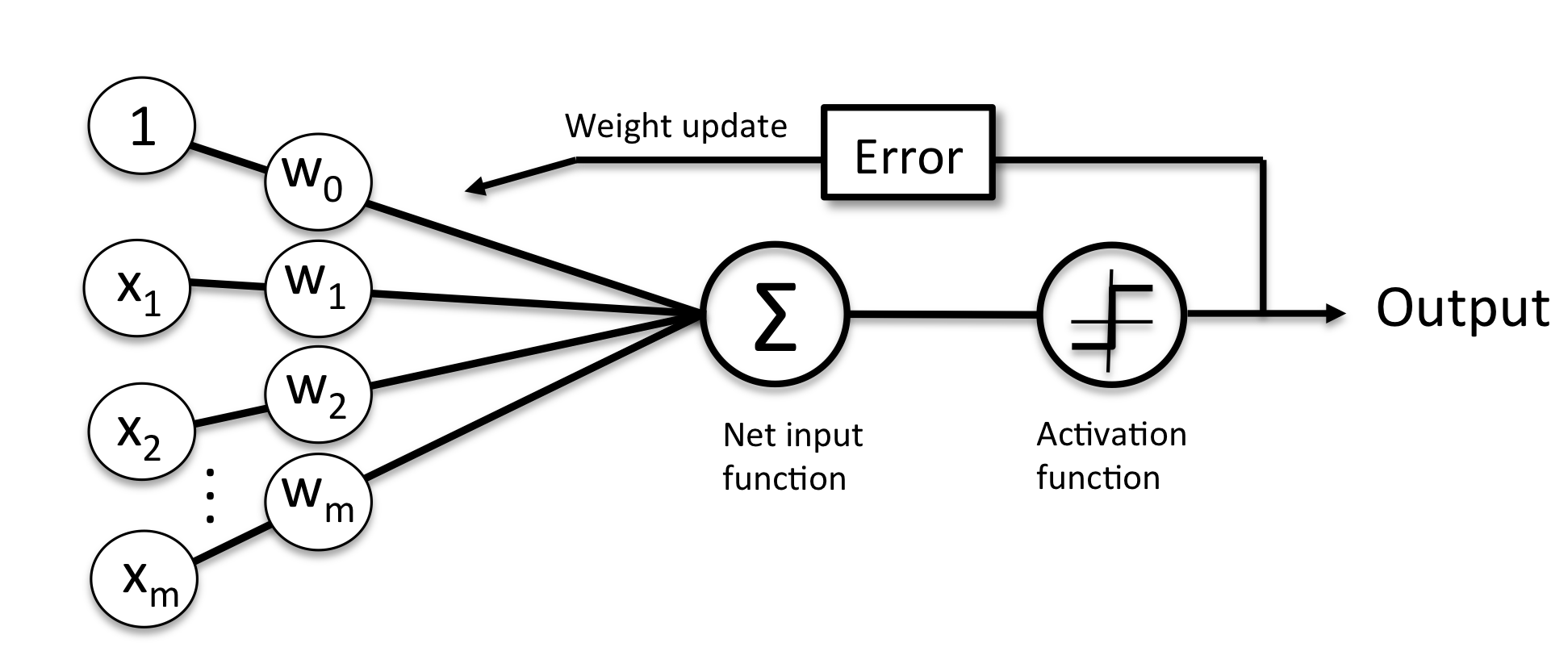(图片来自 python-machine-learning)
感知器算法 1 步骤大致如下：
- 将权重初始化为 0 或一个很小的随机数。
- 对于每个训练样本 $x^{(i)}$ 执行下列操作：
- 计算输出值 $\hat{y}$ 。
- 更新权重。
这里的输出值, 就是由我们预先定义的单位阶跃函数 (unit step function) 所预测得出的类别标签。权重向量 $\mathbf{w}$ 中的每一个权重 $w_j$ 的更新公式为：
\begin{equation} w_j := w_j + \Delta w_j \end{equation}
$\Delta w_j$ 被用来更新权重 $w_j$ , 其计算公式如下：
\begin{equation} \Delta w_j = \eta \left(y^{(i)} - \hat{y}^{(i)}\right)x_j^{(i)} \end{equation}
import numpy as np
class Perceptron(object):
"""Perceptron classifier.
Parameters
----------
eta: float
Learning rate (between 0.0 and 1.0)
n_iter: int
Passes over the training dataset.
Attributes
----------
w_: 1d-array
Weights after fitting.
errors_: list
Number of misclassifications in every epoch.
"""
def __init__(self, eta=0.01, n_iter=10):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
"""Fit training data.
Parameters
----------
X: {array-like}, shape = [n_samples, n_features]
Training vectors, where n_samples is the number of samples
and n_features is the number of features.
y: array-like, shape = [n_samples]
Target values
Returns
-------
self: object
"""
self.w_ = np.zeros(1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
# 公式 2 : update = \Delta \mathbf{w}
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.net_input(X) >= 0.0, 1, -1)
参考资料:
⤧ Next post 偏差与方差 ⤧ Previous post 理解梯度下降