理解梯度下降
本文最初写于 2016 年 4 月发表于我的博客, 当时只是大略地给出了渐进理解的轮廓,很多内容也是粗糙的很,今天在这里重新梳理一遍。
什么是梯度下降?可以先从这里 Gradient descent 或 梯度下降法 了解其基本概念。
刚接触这个概念时,很多人会告诉我们这样一个结论:沿着梯度相反的方向函数下降地最快. 而当我们追问为什么是如此时,恐怕很多人便开始说不清,道不明了。当然,这完全可以从严格的数学证明角度进行解释,但是有没有稍微直观点的方式进行理解呢?
下面我试图从一些所涉及到一些数学最基本概念的物理意义上进行解释,如有谬误,欢迎来信纠正。
什么是梯度
直接问梯度是什么,可能有些人会不知道怎么回答,下面给出两个选项:
- 梯度是一个数 (没有方向)
- 梯度是一个向量 (有方向)
直接上结论, 梯度是一个有方向的向量, 带着这个概念再来慢慢理解.
导数
导数的几何意义可能很多人都比较熟悉: 当函数定义域和取值都在实数域中的时候,导数可以表示函数曲线上的切线斜率。 除了切线的斜率,导数还表示函数在该点的变化率。

导数的物理意义表示函数在这一点的 (瞬时) 变化率。
偏导数
既然谈到偏导数,那就至少涉及到两个自变量,以两个自变量为例,$z = f(x, y)$ . 从导数到偏导数,也就是从曲线来到了曲面. 曲线上的一点,其切线只有一条。但是曲面的一点,切线有无数条。
因为曲面上的每一点都有无穷多条切线,描述这种函数的导数相当困难。偏导数就是选择其中一条切线,并求出它的斜率。通常,最感兴趣的是垂直于 y 轴(平行于 xOz 平面)的切线,以及垂直于 x 轴(平行于 yOz 平面)的切线。
 (来自维基百科)
(来自维基百科)
一个多变量函数的偏导数是它关于其中一个变量的导数,而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。
偏导数的物理意义表示函数沿着坐标轴正方向上的变化率。
方向导数
方向导数是偏导数的概念的推广, 偏导数研究的是指定方向 (坐标轴方向) 的变化率,到了方向导数,研究哪个方向可就不一定了。
一个标量场在某点沿着某个向量方向上的方向导数,描绘了该点附近标量场沿着该向量方向变动时的瞬时变化率。这个向量方向可以是任一方向。
方向导数的物理意义表示函数在某点沿着某一特定方向上的变化率。
梯度
说完方向导数,终于要谈到梯度了。
在一个数量场中,函数在给定点处沿不同的方向,其方向导数一般是不相同的。那么沿着哪一个方向其方向导数最大,其最大值为多少,这是我们所关心的,为此引进一个很重要的概念: 梯度。
假设函数在其一点 $p_0$ 处,那么它沿哪一方向函数值增加的速度能够最快?
摘自 梯度 维基百科:
在向量微积分中,标量场的梯度是一个向量场。标量场中某一点的梯度指向在这点标量场增长最快的方向(当然要比较的话必须固定方向的长度),梯度的绝对值是长度为1的方向中函数最大的增加率。以另一观点来看,由多变数的泰勒展开式可知,从欧几里得空间 $R^n$到 $R$ 的函数的梯度是在 $R^n$ 某一点最佳的线性近似。在这个意义上,梯度是雅可比矩阵的一个特殊情况。
- 在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。
- 梯度一词有时用于斜度,也就是一个曲面沿着给定方向的倾斜程度。可以通过取向量梯度和所研究的方向的内积来得到斜度。梯度的数值有时也被称为梯度。
为什么沿着梯度方向函数增长最快
下面对为什么沿着梯度的方向函数增长最快进行证明:
证明准备
方向导数定义:

方向导数公式:
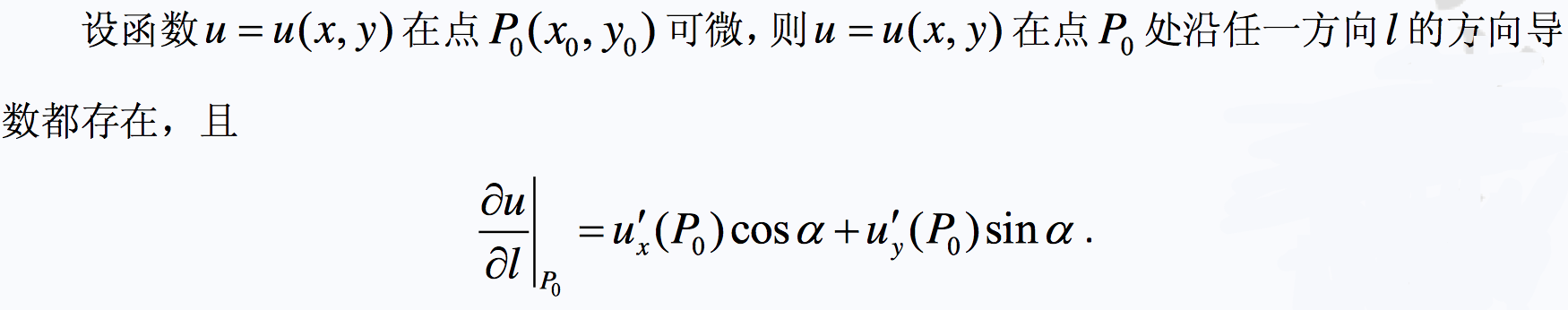
梯度公式: 
从方向导数与梯度进行证明
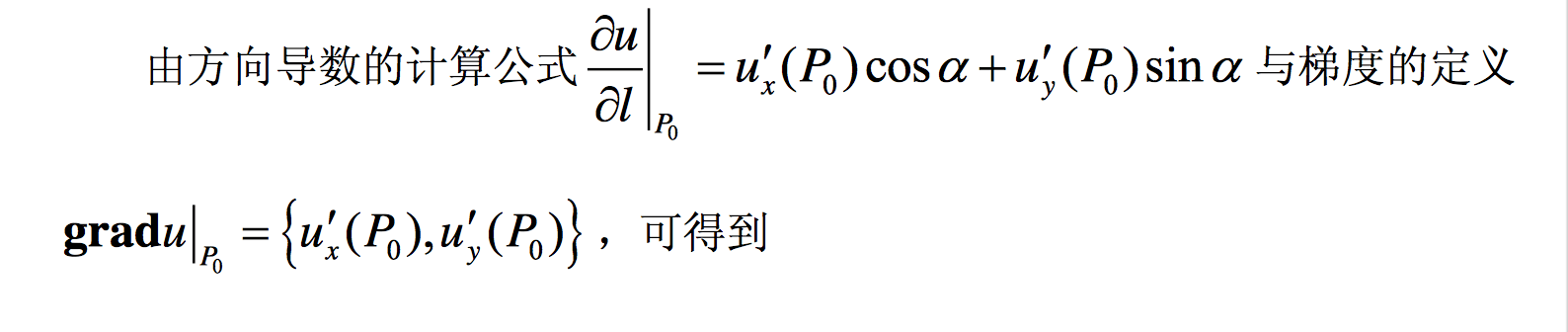

总结
| 概念 | 物理意义 |
|---|---|
| 导数 | 函数在该点的瞬时变化率 |
| 偏导数 | 函数在坐标轴方向上的变化率 |
| 方向导数 | 函数在某点沿某个特定方向的变化率 |
| 梯度 | 函数在该点沿所有方向变化率最大的那个方向 |
函数在某一点处的方向导数在其梯度方向上达到最大值,此最大值即梯度的范数。
这就是说,沿梯度方向,函数值增加最快。同样可知,方向导数的最小值在梯度的相反方向取得,此最小值为最大值的相反数,从而沿梯度相反方向函数值的减少最快。更多内容可见:方向导数与梯度。
在机器学习中往往是最小化一个目标函数 $L(\Theta)$,理解了上面的内容,便很容易理解在梯度下降法中常见的参数更新公式: \[\Theta = \Theta - \gamma \frac{\partial L}{\partial \Theta}\]
$\gamma$ 在机器学习中常被称为学习率 ( learning rate ), 也就是上面梯度下降法中的步长。
通过算出目标函数的梯度(算出对于所有参数的偏导数)并在其反方向更新完参数 $\Theta$ ,在此过程完成后也便是达到了函数值减少最快的效果,那么在经过迭代以后目标函数即可很快地到达一个极小值。如果该函数是凸函数,该极小值也便是全局最小值,此时梯度下降法可保证收敛到全局最优解。
概念上大概理解了梯度下降,下一步便是写点代码来理解一下了,毕竟上面所述还是有些过于理论,有时间我会从代码实现与分析中进一步理解梯度下降, 敬请期待。